
1 Postgrado en Ingeniería Agrícola y Uso Integral del Agua-Universidad Autónoma Chapingo. Carretera México-Texcoco, km. 38.5. Chapingo, Texcoco Estado de México. C. P. 56230. Tel: 595 95 215 51. (ilopez@correo.chapingo.mx; ariasar_mx@yahoo.com.mx).
Se analizaron mediante pruebas de microscopía y en túnel de viento, las características geométricas, porosidad y la caída de presión, respectivamente de siete diferentes mallas comúnmente usadas como barreras físicas en ventanas de invernaderos mexicanos para determinar su efecto sobre la tasa de ventilación, la permeabilidad y el factor inercial. Las mallas se analizaron en la Universidad Autónoma Chapingo en mayo de 2013 y fueron: anti-trips (M1), anti-trips bicolor (M2), anti-áfidos (M3), anti-áfidos bicolor (M4), cenital (M5), rompevientos verde-negro (M6) y anti-áfidos blanca (M7), cuyas porosidades fueron 0.36, 0.35, 0.47, 0.45, 0.54, 0.29 y 0.43 respectivamente. La geometría de las mallas se realizó midiendo las áreas de los poros con un microscopio óptico, para determinar las porosidades y calcular el descenso de la tasa de ventilación. Posteriormente, las características aerodinámicas más importantes; es decir, permeabilidad y factor inercial, se determinaron usando un túnel de viento para medir la relación entre la caída de presión causada por cada malla y la velocidad del flujo de aire. Los resultados mostraron que la malla cenital (M5) presenta la menor resistencia al flujo de aire con 21% de descenso en la tasa de ventilación, mientras que la malla rompevientos verde-negra (M6) fue de 50%. Los invernaderos en México normalmente usan la malla del tipo anti-áfidos con porosidad entre 0.43 y 0.47 para las ventanas laterales y cenitales.
Palabras clave: caída de presión; factor inercial; permeabilidad; porosidad
INTRODUCCIÓN
La producción de hortalizas en ambientes protegidos de los trópicos húmedos y en climas cálidos, es vulnerable al estrés climático (valores elevados de temperatura y humedad), plagas y a las enfermedades virales trasmitidas por ellas (von Zabeltitz, 2011). El uso de mallas plásticas en ventanas de invernaderos, macrotúneles y malla- sombra, se recomienda para prevenir daños importantes de los cultivos a causa de insectos (Romero-Gómez et al., 2010). Su principal función es ejercer como barrera física que impide la entrada de insectos al interior del invernadero y por lo tanto, una baja incidencia de enfermedades, minimizando la necesidad de tratamientos fitosanitarios (Álvarez et al., 2006). El uso de mallas está muy difundido, pero tienen una influencia negativa haciendo descender las tasa de ventilación natural, y por tanto, aumentan la temperatura y la humedad al interior de ambientes protegidos (Valera et al., 2006).
La eficiencia de estas mallas depende principalmente del tamaño del mallado (debe ser menor al diámetro torácico del insecto más pequeño que se quiere excluir), su sección transversal y propiedades ópticas (tales como el color) (Teitel, 2007; von Zabeltitz, 2011; Castilla, 2013). La porosidad de la malla es la relación entre el área de los poros y el área total; depende del diámetro del hilo y del número de hilos por unidad de área, y determina la reducción en la tasa de ventilación natural (Castilla, 2013).
Debido a esta resistencia la velocidad del aire, la temperatura y la humedad en el interior de los invernaderos son modificadas (Fatnassi et al., 2003) y se reduce la transmisión de luz (von Zabeltitz, 2011), afectando negativamente el crecimiento y desarrollo del cultivo, y favoreciendo la aparición de enfermedades (Teitel et al., 2008). Las mallas empleadas normalmente en invernaderos disminuyen la tasa de ventilación aproximadamente 40% en mallas anti-insectos, y 70-80% en mallas anti-trips (Montero y Antón, 2000), aunque esta disminución puede ser más alta si la velocidad del viento es muy baja (Castilla, 2013).
Para analizar las características del flujo de aire que atraviesa las mallas empleadas habitualmente en invernaderos es importante determinar su permeabilidad (K, m2) y su factor inercial (Y, adimensional), dos parámetros fundamentales para poder modelar el paso de aire a través de un medio poroso. Así, Miguel et al. (1997) y Miguel et al. (1998) evaluaron diferentes mallas en un túnel de viento, y encontraron que las mejores correlaciones con la porosidad son las de la ecuación (1):
Donde: α= porosidad de la malla (m2 m-2).
Por su parte, Valera et al. (2005) estudiaron 11 mallas en un túnel de viento y encontraron las siguientes correlaciones (ecuación 2):
En los estudios de Miguel et al. (1997), Miguel et al. (1998) y Valera et al. (2005), la caída de presión fue graficada como una función de la velocidad del aire antes de la malla, y un polinomio de segundo grado fue ajustado a la curva de medición, para calcular la permeabilidad y el factor inercial (Teitel, 2010). Al respecto, Flores-Velázquez y Montero (2008) propusieron diferentes relaciones para K e Y (ecuación 3), basados en datos publicados por Miguel et al. (1997), Teitel (2001) y Valera et al. (2006).
Cuando las ecuaciones de Navier-Stokes, son resueltas numéricamente en simulaciones de dinámica de fluidos computacional (CFD), el término fuente en la ecuación de momento está representado por la ecuación de Forchheimer. Diferentes autores (Campen y Bot, 2003; Fatnassi et al., 2003; Molina-Aiz et al., 2004) usan esta aproximación para determinar los valores de K e Y.
El objetivo del estudio fue analizar mediante mediciones microscópicas y en túnel de viento, la porosidad y caída de presión, respectivamente, de siete mallas comerciales usadas habitualmente en ventanas de invernaderos mexicanos, para determinar, su efecto sobre las tasas de ventilación, la permeabilidad y el factor inercial de cada una de ellas.
MATERIALES Y MÉTODOS
Sitio experimental
El estudio se realizó durante el 2013 en los laboratorios de Energía del DIMA, y laboratorio de Ingeniería de la Madera de DICIFO de la Universidad Autónoma Chapingo (UACH), en Chapingo, México. Se realizaron mediciones microscópicas de la geometría de los poros de diferentes mallas con un microscopio óptico (Leica Microsystems modelo DM500). Y pruebas experimentales en un túnel de viento C15-10 (Armfield Inc. NJ, USA) para determinar la caída de presión en diferentes mallas.
Caracterización geométrica de las mallas
Selección y preparación de las muestras. Las muestras de las mallas anti-trips (M1), anti-trips bicolor (M2), anti-áfidos (M3), anti-áfidos bicolor (M4), cenital (M5), rompevientos verde-negro (M6) y anti-áfidos (M7), se seleccionaron de manera aleatoria en productos nuevos comercializados por empresas fabricantes de fibras plásticas y constructores de invernaderos en México. La preparación de las muestras consistió en colocar una pequeña porción rectangular de cada malla analizada a lo largo de toda la superficie de un portaobjetos para microscopio, sujetada por cinta trasparente. De este modo, la malla se ajusta a un plano y se asegura que la región explorada sea la misma para todas las muestras. Se analizaron cinco superficies seleccionadas aleatoriamente de cada malla. Las áreas de cada muestra fueron de 2.5 mm2 tomadas con un objetivo a 4 x de un microscopio óptico (Leica Microsystems modelo DM500) y una cámara ICC50 Leica de 3 megapíxeles.
Procesamiento de las imágenes. Se usó el software Leica Application Suite (LAS) EZ para simplificar el control de la cámara, la captura de imágenes, la anotación, la medición y la documentación. Las muestras digitalizadas fueron convertidas de imágenes en escala de grises a blanco y negro. Después se realizaron las mediciones marcando con el apuntador del ratón el interior del poro tanto en dirección vertical como horizontal para obtener las dimensiones de éste y, en los bordes de los hilos para determinar su diámetro (Figura 1).

Figura 1 Muestras de malla usada para determinar el tamaño de poros y diámetro de hilos. Bases del método.
Se seleccionó una metodología de análisis geométrico ampliamente utilizada en diversos trabajos de reportados sobre caracterización geométricas de mallas anti-insectos (Cabrera et al., 2006; Álvarez et al., 2012). Mediante la toma de imágenes digitales de muestras usando un microscopio óptico. La base geométrica es considerar que cada orificio (poro) de la malla representa un paralelogramo que está definido por cuatro hilos monofilamentos que se entrelazan entre sí para formar la red o malla. Finalmente, se determina la porosidad con base en la relación que existe entre el área de poros y el área total de mallas.
Número de hilos por unidad de longitud. De acuerdo con Cabrera et al. (2006), se considera que las mallas anti- insectos comúnmente empleadas en los invernaderos por lo general son fabricadas con un solo tipo de hilo de diámetro constante D (mm), y conociendo el número de hilos cm-1 en las dos direcciones X e Y (NX, NY), el tamaño promedio del poro en ambas direcciones LX (mm) y LY (mm) se puede calcular usando las ecuaciones (4) y (5):
Álvarez et al. (2012), extendiendo su análisis a mallas que pueden tener un diámetro de hilo distinto en las direcciones de la trama y de la urdimbre, propone que el número de hilos por unidad de longitud (hilos cm-1) en las direcciones trama (ρx) y urdimbre (ρy) de la malla se calcula usando las ecuaciones (6) y (7):
Donde: lpy y lpx= Las dimensiones características de los poros de la malla; dhx y dhy= espesor de los hilos del trama y urdimbre, respectivamente.
Cálculo de la porosidad. La separación de los hilos que forman el tejido de una malla anti-insectos define una matriz porosa formada por filas y columnas de poros. Esta puede ser observada mediante un microscopio como una superficie plana. Una de las propiedades geométricas más importantes de estos materiales es su porosidad α (m2 m-2) definida como la superf icie ocupada por los orif icios con respecto a la superficie total de la malla (Álvarez et al., 2012; Cabrera et al., 2006; Valera et al., 2006 y puede ser calculada por la ecuación (8) para una malla con mismo tipo de hilo en ambas direcciones de tejido.
Reducción de la tasa de ventilación. La reducción de la tasa de ventilación (R, %), que provocan las mallas usadas en ventanas de ambientes protegidos se puede determinar por medio de la ecuación empírica (9) propuesta por Pérez-Parra et al. (2004).
Donde: Φ= Flujo de aire volumétrico a través de una ventana con malla (m3 s-1); Φm= flujo de aire volumétrico a través de una ventana sin malla (m3 s-1).
Caracterización aerodinámica de las mallas. Se utilizó el túnel de viento C15-10 (Armfield Inc. NJ, USA), el cual cuenta con una sección de trabajo en material acrílico trasparente de (150 mm x 150 mm x 455 mm) y ventilador (Ziehl-Abegg modelo THCL155 IP54) de corriente alterna (CA) controlado por inversor que permite un control preciso de la velocidad del aire hasta 34 m s-1 libre de obstáculos. El aire fluye a través de la sección de trabajo impulsado por un ventilador de velocidad variable situado en el extremo de la salida del túnel. Incorpora un enderezador de flujo tipo panal en la entrada, y la relación de contracción de 9.4:1 asegura un flujo de aire continuo a través de la sección de trabajo.
Preparación e instalación de las muestras en túnel de viento. Las muestras utilizadas en el túnel de viento se cortaron y se colocaron sobre un marco metálico. El marco se construyó con aluminio de las mismas dimensiones que la sección transversal del túnel de viento (150 mm x 150 mm) en la zona de trabajo. Las mallas se colocaron y tensaron mediante un dispositivo de sujeción en todo el perímetro del marco para simular colocada en los invernaderos. Después las muestras se instalaron en la parte central de la sección de trabajo del túnel de viento para realizar las pruebas.
Operación del túnel de viento. Una vez instalada la muestra de la malla en la sección de trabajo del túnel de viento, se instaló el sensor de presión electrónico (0 - 178 mm H2O) en la pared de la sección de trabajo antes y después de la malla, para realizar las mediciones de la presión estática y velocidad del aire. La operación del túnel de viento se llevó a cabo usando la interfaz Armfield IFD7, que permite la conexión túnel de viento-computadora personal. Mediante el programa de computadora C15-304 se realizó el control del ventilador en el túnel de viento, incluyendo su encendido y control de la velocidad de rotación entre de 0 a 100% (de 0 a 34 m s-1) para visualizar y registrar todos los datos que se presentan en el interior del túnel de viento. Al término de la prueba se redujo la velocidad de rotación gradualmente hasta 0 % para apagar el ventilador.
Registro de datos. Las mediciones de presión estática y velocidad del aire durante las pruebas se registraron en una hoja de cálculo para su posterior análisis, se consideró un tiempo de muestreo de 2 min por cada incremento en 1% de la velocidad de rotación del ventilador.
Algoritmo para calcular la caída de presión. Miguel et al. (1997) analizaron el flujo de aire a través de mallas utilizando las ecuaciones de flujo en medios porosos. Para el estado estacionario, el flujo de f luido incompresible a través de un material poroso, la caída de presión puede ser expresada por la ecuación de Forchheimer (10):
Donde: μ= viscosidad dinámica (kg m-1 s-1); u= velocidad del aire (m s-1); ρ= densidad del aire (kg m-3); K y Y= permeabilidad y el factor inercial de la malla respectivamente.
Experimentalmente es posible determinar las características aerodinámicas (permeabilidad K y factor inercial Y) de las mallas mediante el siguiente procedimiento:
Paso 1. Los datos de presión y velocidad de aire medidos en el túnel de viento se ordenan en una matriz de dos columnas (presión y velocidad) y n filas (número de datos), para ser graficados (caída de presión contra velocidad del aire) y ajustar a un modelo o polinomio de segundo grado.
Paso 2. Mediante la interface gráfica de la herramienta de ajuste de curvas de MATLAB (cftool, Curve Fitting Tool) se importan los datos del espacio de trabajo de MATLAB a la herramienta cftool.
Paso 3. Los datos se exploran gráficamente para posteriormente ajustarlos usando un modelo paramétrico de segundo grado (ΔP=AV2+BV+C), de la librería de cftool y generar sus estadísticas.
El modelo de segundo grado es relacionado con la ecuación de Forchheimer de la siguiente manera:
En la cual los coeficientes (A y B) pueden ser calculados en función de la ecuación (11).
A partir de (13) es posible calcular la permeabilidad, usando la ecuación (14).
Similar procedimiento se sigue para Y con la ecuación (15).
La permeabilidad específica del medio representa la capacidad de permitir el paso de un fluido a través y es función de la viscosidad y de la frecuencia de contacto con las paredes sólidas. El coeficiente de arrastre (Y) está influenciado por la naturaleza del medio, en este caso poroso, que define dicho factor inercial. Se asume una densidad del aire de (ρ) = 1.204 kg m-3 y una viscosidad dinámica (μ) = 1.7894 x10-5 [Kg m-1 s-1], ambas para ser usadas en las ecuaciones 12, 13, 14 y 15.
Análisis estadístico
Para determinar la diferencia significativa estadísticamente para las mallas en cuanto a la porosidad se realizó un ANDEVA donde se consideraron siete muestras con cinco repeticiones cada una. Los datos obtenidos en promedios de características geométricas y aerodinámicas se realizaron pruebas de comparación de medias de Tukey (p≤ 0.05) usando el paquete estadístico SAS 9.2 (SAS, 2009). Los datos obtenidos de características aerodinámicas se analizaron usando la herramienta cftool del programa Matlab para generar los modelos de regresión lineal de segundo grado y ajustar a los resultados obtenidos de la caída de presión y velocidad del aire (0 - 4 ms-1, 0 - 6 ms-1 y 0 - 8 ms-1), donde su mejor ajuste fue evaluado con base a la raíz del error cuadrático medio (RMSE), suma de los cuadrados debido al error (SSE) y coeficiente de determinación (R2).
RESULTADOS Y DISCUSIÓN
Características geométricas de las mallas
En el Cuadro 1 se muestran los promedios del diámetro de hilo, longitudes en ambas direcciones de los poros, la porosidad y la reducción de la tasa de ventilación para las siete mallas estudiadas. La porosidad presentó cuatro agrupaciones entre sí, destacando las mallas anti-trips M1 y M2; las anti-áfidos M3, M4 y M7; la cenital M5 y la rompevientos M6, obteniendo diferencias significativas entre tipos de mallas. La malla cenital fue la más porosa; es decir, presenta menos resistencia al flujo de aire a su paso por ella. Este tipo de malla se coloca en las ventanas cenitales de los invernaderos debido a que allí se presenta alta velocidad de aire, lo que no permite el flujo de los insectos hacia el interior del invernadero.
Cuadro 1 Características geométricas de mallas típicas de invernaderos mexicanos.
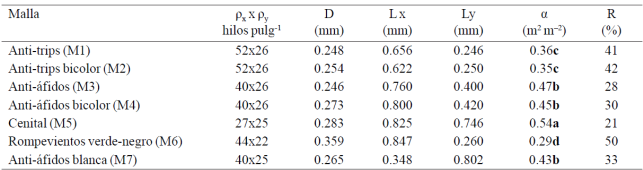
Medias con distinta letra en una hilera son estadísticamente diferentes (Tukey, p≤ 0.05). ρx y ρy= número de hilos por pulgada cuadrada en la dirección x y y; D= diámetro de hilo; Lx y Ly= longitud en la dirección x y y del poro; α= porosidad; R= reducción de la tasa de ventilación.
Romero-Gómez et al. (2010) mencionan que cuando las ventanas cenitales se ubican a sotavento aunque algunas actúan como entradas del aire, las restantes funcionan como salidas de aire; el aire que entra a través de las ventilas cenitales proporciona poca aeración en la zona de las plantas, en cambio se desarrolla alta velocidad de aire justo en su parte superior del invernadero. Este fenómeno se presenta debido a las características geométricas de la malla usada en ventanas de invernaderos. Los invernaderos en México normalmente usan la malla del tipo anti-áfidos con porosidad entre 43 y 47% para las ventanas laterales y cenitales.
Por otra parte, las mallas con mayor resistencia son la rompevientos y las anti-trips. Las primeras tienen la finalidad de reducir los efectos nocivos al cultivo por acción mecánica de flujos altos de viento, reduciendo su velocidad en el interior del invernadero; las segundas son utilizadas en ventanas laterales para prevenir daños importantes a los cultivos causadas por insectos plaga de reducido tamaño, particularmente diseñadas para prevenir el ingreso de trips (por ejemplo, Frankliniella occidentalis). Las mallas anti-áfidos son las más usadas en invernaderos mexicanos porque están diseñadas para prevenir la entrada de áfidos (Aphis gossypii) y mosquitas blancas (por ejemplo, Bemisia argentifolii, Trialeurodes vaporariorum, B. tabaci) (Teitel, 2007; Romero-Gómez et al., 2010) que son los principales insectos trasmisores de enfermedades virales.
Características aerodinámicas de las mallas
La Figura 2 muestra el comportamiento completo de la caída de presión en función de la velocidad del aire producida en el túnel de viento a velocidad de rotación de su ventilador de 0 a 100%. La malla rompevientos verde-negro, fue la menos porosa, presentó una caída de presión de 459.9 Pa y alcanzó una velocidad máxima de 8.5 m s-1 en el túnel de viento. A diferencia de la malla cenital que fue la más porosa, presentó una caída de presión de 371.7 Pa logrando una mayor velocidad de aire de 15.9 m s-1 en el túnel. La zona centro de México presenta una velocidad de viento máximas promedio de 8.1 m s-1, registradas en el Aeropuerto Internacional de la Ciudad de México, D. F., en febrero durante el periodo de 2001 a 2008.
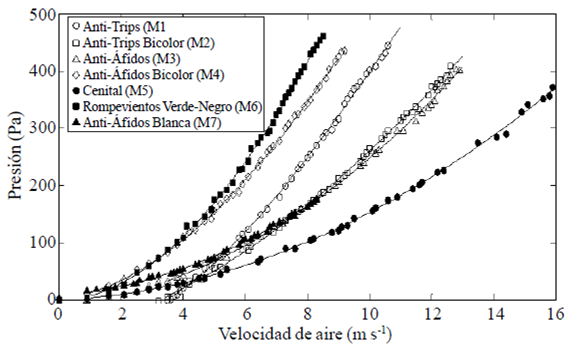
Figura 2 Caída de presión en función de velocidad del aire medida en túnel de viento para siete mallas anti- insectos.
Tomando en cuenta la velocidad de viento máxima que se puede presentar en el Valle de México, se realizaron los análisis a velocidades de aire en el túnel de viento entre flujos de 0 a 4 m s-1, 0 a 6 m s-1 y de 0 a 8 m s-1. Similarmente, Romero-Gómez et al. (2010) analizaron mallas Anti- Insectos a velocidades de 0 a 4 m s-1, y por su parte Valera et al. (2006) velocidades de flujo de aire hasta 7 m s-1.
La Figura 3 presenta la relación entre la caída de presión y velocidad de aire de 0 a 4 ms-1 para las mallas analizadas. De acuerdo con el análisis estadístico se obtuvieron dos agrupaciones con velocidades de hasta 4 ms-1, donde las mallas M1, M2 y M6 tienen una caída de presión promedio de 20.44 Pa, 21.46 Pa y 40.54 Pa respectivamente. Las mallas M3, M4, M5 y M7 con caídas de presión promedio de 14.09 Pa, 14.67 Pa, 9.04 Pa y 14.33 Pa respectivamente, no presentaron diferencias estadísticamente significativas.
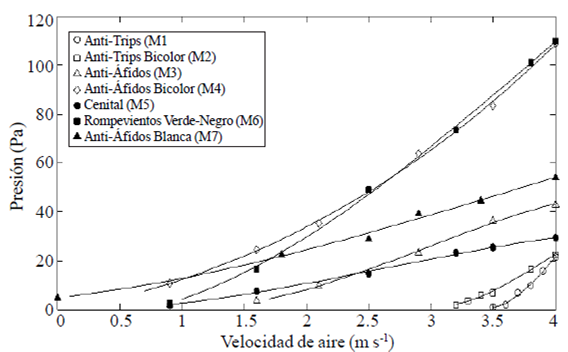
Figura 3 Caída de presión en función de velocidad del aire (0 a 4 m s-1) de siete mallas anti-insectos.
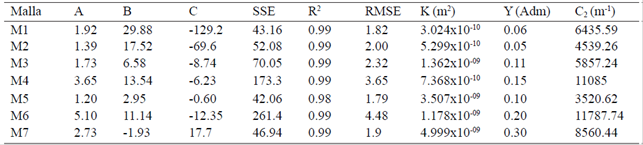
El Cuadro 2 presenta los coeficientes A, B y C, resultado del mejor ajuste de la caída de presión en función de la velocidad del aire de 0 - 4 m s-1, y K, Y y C2 calculados de acuerdo con las Ecuaciones 14, 15 y 16.
Cuadro 2 Coeficientes válidos para velocidad del aire de 0 a 4 m s-1.
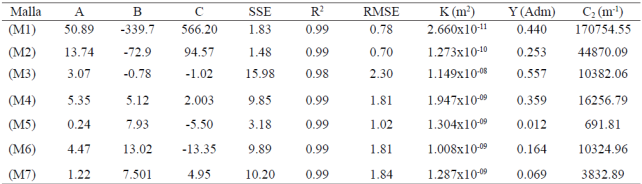
Coeficientes A, B y C para el mejor ajuste de la ecuación (ΔP = Au 2 + Bu + C); RMSE= raíz del error cuadrático medio; SSE= suma de los cuadrados debido al error; R2= coeficiente de determinación; K permeabilidad; Y= factor inercial; C2= coeficiente de perdida inercial.
Para el flujo de velocidad del aire de 0 a 6 ms-1, la caída de presión medida en el túnel de viento (Figura 4), se agrupa en dos categorías estadísticamente diferentes en base a la prueba de Tukey: 1) en el primer grupo, malla M4 y M6 (caídas de presión promedio de 120.05 y 134.28 Pa, respectivamente); y 2) en el segundo grupo, M1, M2, M3, M5 y M7 (caídas de presión promedio de 50.08 Pa, 39.06 Pa, 51.85 Pa, 33.82 Pa, 60.91 Pa, respectivamente).
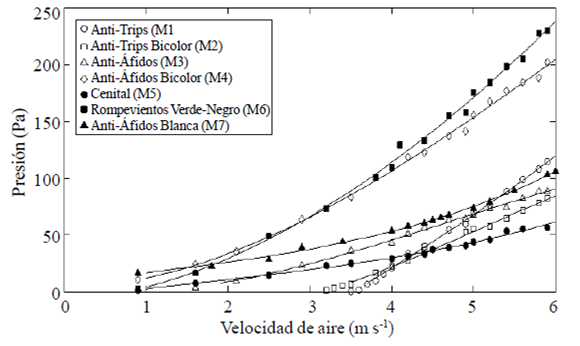
Figura 4 Caída de presión calculada en función de la velocidad del aire (0 a 6 m s-1) para las siete mallas anti-insectos.
Los coeficientes A, B y C del polinomio de segundo grado obtenido del mejor ajuste de las curvas de caída de presión contra velocidad del aire en el flujo de 0 - 6 m s-1, y K, Y y C2 calculados de acuerdo a las ecuaciones 14, 15 y 16, se presentan en el Cuadro 3.
Cuadro 3 Coeficientes válidos para velocidad del aire de 0 a 6 m s-1.
Coeficientes A, B y C para el mejor ajuste de la ecuación (ΔP = Au 2 + Bu + C); RMSE= raíz del error cuadrático medio; SSE= suma de los cuadrados debido al error; R2= coeficiente de determinación; K permeabilidad; Y= factor inercial; C2= coeficiente de perdida inercial.
La Figura 5 muestra las curvas de caída de presión en función de la velocidad del aire de 0 a 8 m s-1, que se agrupan en tres categorías donde presentan diferencias significativas. El primer grupo estuvo integrado por las mallas M4 y M6 con caídas de presión promedio de188.86 Pa y 216.55 Pa, respectivamente; el segundo grupo se integró por M1 y M7 con una caída de presión promedia de 111.69 Pa y 91.95 Pa, respectivamente; y el tercer grupo estuvo conformado por M2, M3 y M5 con caídas de presión promedio de 76.79 Pa, 83.46 Pa y 53.36 Pa, respectivamente.
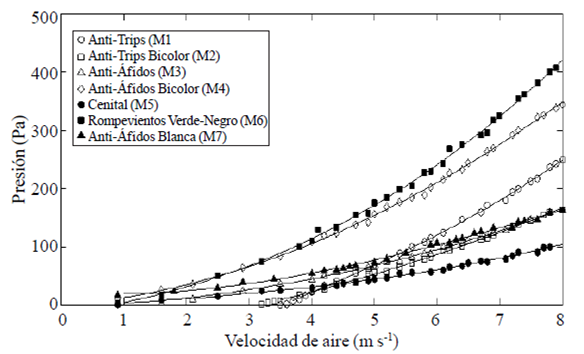
Figura 5 Caída de presión calculada en función de la velocidad del aire (0 a 8 m s-1) para siete mallas anti-insectos.
El Cuadro 4 presenta los coeficientes A, B y C, resultantes del modelo de regresión de segundo grado para las mallas analizadas, válido para velocidades del aire de 0-8 m s-1; también se presentan los coeficientes K, Y y C2, calculados con las ecuaciones 14, 15 y 16, para las siete mallas analizadas. Los resultados obtenidos son similares a los registrados por Álvarez et al. (2006), dado que en su muestra 6 y la M6 del presente estudio, son similares en su valor de porosidad, al obtener un valor de un 20% menos en K y 21% mayor en Y.
Cuadro 4 Coeficientes válidos para velocidad del aire de 0 a 8 m s-1.
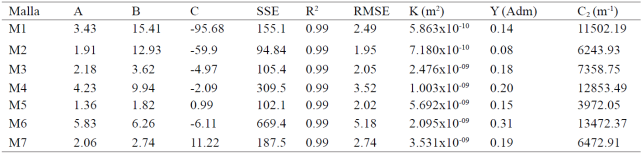
Coeficientes A, B y C para el mejor ajuste de la ecuación (ΔP = Au2 + Bu + C); RMSE= raíz del error cuadrático medio; SSE= suma de los cuadrados debido al error; R2= coeficiente de determinación; K permeabilidad; Y= factor inercial; C2= coeficiente de perdida inercial.
CONCLUSIONES
El análisis geométrico permitió determinar las porosidades de siete mallas con el fin de estimar la reducción en la tasa de ventilación. La porosidad de las mallas osciló entre 0.29 a 054, para una reducción teórica en los valores de tasa de ventilación entre 21 y 50%, respectivamente. Las características aerodinámicas de las mallas analizadas son afectadas por la velocidad del flujo de aire, obteniendo valores promedio de permeabilidad (2.186 x 10-09) y factor inercial (0.194). A velocidades menores de 4 m s-1 las mallas mostraron dos agrupaciones con diferencia significativa. a) anti-trips y rompevientos; y b) anti-áfidos y cenital. A velocidades de 6 a 8 ms1, hubo tres categorías con diferencias significativas. a) rompevientos; b) anti-trips; y c) anti-áfidos y cenitales.
AGRADECIMIENTOS
Los autores desean expresar su reconocimiento al Laboratorio de Energía del DIMA, y al Laboratorio de Ingeniería de la Madera de DICIFO de la Universidad Autónoma Chapingo, por el apoyo brindado mediante sus equipos (túnel de viento y microscopio).
LITERATURA CITADA
Álvarez, A. J.; Valera, D. L. and Molina-Aiz, F. D. 2006. A method for the analysis of the geometric characteristics of protection screens. Acta Hortic. 719:557-564. [ Links ]
Álvarez, A. J.; Oliva, R. M. and Valera, D. L. 2012. Software for the geometric characterization of insect-proof screens. Comp. Electr. Agric. 82:134-144. [ Links ]
Cabrera, F. J.; López, J. C.; Baeza, E. J. and Pérez-Parra, J. 2006. Efficiency of anti-insect screens placed in the vents of Almería greenhouses. Acta Hortic. 719:605-614 [ Links ]
Campen, J. B. and Bot, G. P. A. 2003. Determination of greenhouse specific aspects of ventilation using three dimensional computational fluid dynamics. Bios. Eng. 84(1):69-77. [ Links ]
Castilla, N. 2013. Greenhouse technology and management. CABI. Second Edition. Boston, MA, USA. 143 p. [ Links ]
Fatnassi, H.; Boulard, T. and Bouirden, L. 2003. Simulation of climatic conditions in full-scale greenhouse fitted with insect-proof screens. Agric. For. Meteorol. 118(1):97-111. [ Links ]
Flores-Velázquez, J. and Montero, J. I. 2008. Computational fluid dynamics CFD study of large scale screenhouses. Acta Hortic. 797:117-122. [ Links ]
Miguel, A. F.; Van de Braak, N. J. and Bot, G. P. A. 1997. Analysis of the airflow characteristics of greenhouse screening materials. J. Agric. Eng. Res. 67(2):105-112. [ Links ]
Miguel, A. F.; Van de Braak, N. J.; Silva, A. M. and Bot, G. P. A. 1998. Physical modeling of natural ventilation through screens and windows in greenhouses. J. Agric. Eng. Res. 70(2):165-176. [ Links ]
Molina-Aiz, F. D.; Valera, D. L. and Álvarez, A. J. 2004. Measurement and simulation of climate inside Almeria-type greenhouse using computational fluid dynamics. Agric. For. Meteorol. 125(1):33-51. [ Links ]
Montero, J. I. and Antón, A. 2000. Buoyancy driven ventilation in tropical greenhouses. Acta Hortic. 534:41-55. [ Links ]
Pérez-Parra, J.; Baeza, E.; Montero, J. I. and Bailey, B. J. 2004. Natural ventilation of parral greenhouses. Biosystems Eng. 87(3):355-366. [ Links ]
Romero-Gómez, P.; Choi, C. Y. and Lopez, C. I. L. 2010. Enhancement of the greenhouse air ventilation rate under climate conditions of central Mexico. Agrociencia. 44(1):1-15. [ Links ]
SAS Institute. 2009. SAS user’s guide. Statistics. Version 8. SAS Inst., Cary, NC. USA. Quality, and elemental removal. J. Environ. Qual. 7886p. [ Links ]
Teitel, M. 2001. The effect of insect-proof screens in roof openings on greenhouse microclimate. Agric. For. Meteorol. 110(1):13-25. [ Links ]
Teitel, M. 2007. The effect of screened openings on green house microclimate. Agric. For. Meteorol. 143(3):159-175. [ Links ]
Teitel, M. 2010. Using computational fluid dynamics simulations to determine pressure drops on woven screens. Bios. Eng. 105(2):172-179. [ Links ]
Teitel, M.; Liron, O.; Haim, Y. and Seginer, I. 2008. Flow through inclined and concertina-shape screens. Acta Hortic. 801:99-106. [ Links ]
Valera, D. L.; Molina-Aiz, F. D.; Álvarez, A. J.; López, J. A.; Terres- Nicoli, J. M. and Madueno, A. 2005. Contribution to the characterization of insect-proof screens: experimental measurements in wind tunnel and CFD simulations. Acta Hortic. 691:441-448. [ Links ]
Valera, D. L.; Álvarez, A. J. and Molina, F. D. 2006. Aerodynamic analysis of several insect-proof screens used in greenhouses. Spanish J. Agric. Res. 4(4):273-279. [ Links ]
Von-Zabeltitz, C. 2011. Integrated greenhouse systems for mild climates: climate conditions, design, construction, maintenance, climate control. Springer. New York. USA. 233-250 pp. [ Links ]
Recibido: Diciembre de 2015; Aprobado: Marzo de 2016
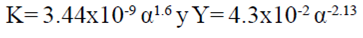
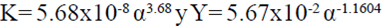
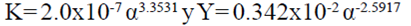
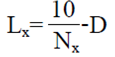
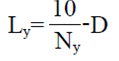
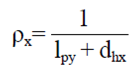
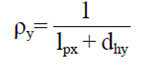
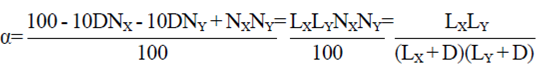
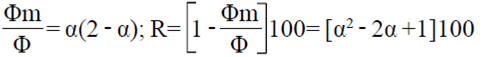
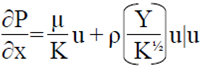
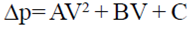
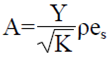
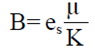
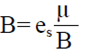
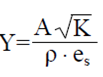
Comentarios
Publicar un comentario